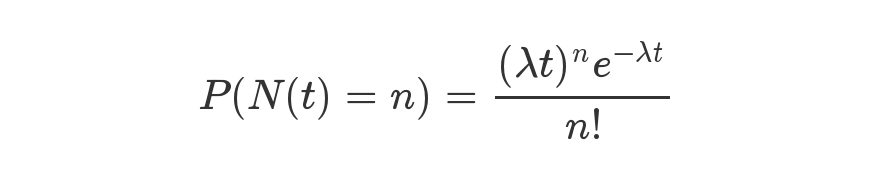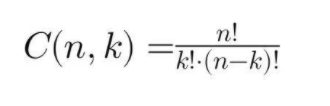语言
<< 返回文章列表

深入解析分布式存储软件 zStorage 的9个9数据可靠性

2025年3月10日
分
布
式
存
储
,
可
靠
性
设
计
,
数
据
可
靠
性
,
z
S
t
o
r
a
g
e
,
技
术
干
货
熊军
74
 
早前发表的《zStorage 的IO流程和路径解析》一文中曾提到，在采用3副本的存储池配置的情况下，zStorage 实现了全年高达9个9的数据可靠性。9个9的可靠性是什么概念呢？反过来说即是1e-9的损坏概率，意味着平均每10亿年才会遇到1次损坏事件。
当然这一数据可靠性是一个理论值，但是理论为实践指明了方向，在实际应用中向理论趋近，结果自然更优。

有朋友可能会问，9个9的数据可靠性的理论值（即1e-9的数据损坏概率）是如何计算得来的？本文详细讲解一下。

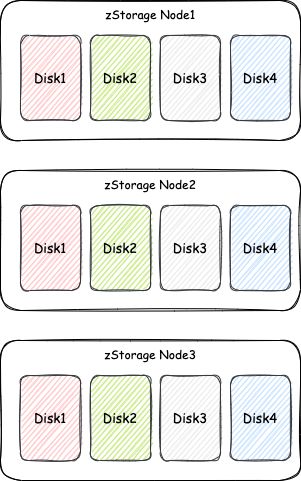
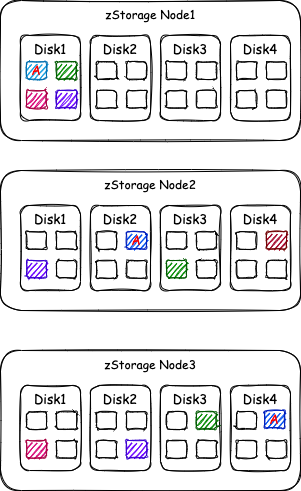
直觉上，对于3副本存储池，数据丢失/损坏的概率，就是“同时发生3块磁盘损坏”的概率，我们口头上也经常这样表达。先来看这个“同时”指什么？它是绝对意义上的同时发生，还是在1秒之内发生叫“同时”，亦或是1分钟之内发生叫“同时”？这个“同时发生3块磁盘损坏”可以定义为“在第一个磁盘损坏后，还没有完成该盘的重构的这段时间内又相继损坏了两个盘”。对于 zStorage 的标准3副本存储池而言，假设磁盘都是4TB大小，磁盘损坏后重构的时间为60分钟，那么：

  • 磁盘1损坏，马上将该磁盘离线，开始重构。

  • 假设又过了10分钟，磁盘2损坏，该磁盘马上进入离线状态，开始对该盘的副本进行重构。

  • 在从磁盘1损坏开始的60分钟（即60分钟的磁盘重构时间）内，磁盘3损坏，这个时间磁盘1的重构还没有完成，磁盘2也还在重构中，这个时候磁盘3再损坏，整个存储池就坏了。
在 zStorage 存储中，重构速率可以达到4TB/h，所以1个4TB的盘重构时间为1小时。结论就是对于4TB大小的盘，在60分钟之内坏了3块，数据就会因损坏而丢失。
结论一：3个磁盘“同时”损坏的概率就是在完成重构1个盘的时间段内连续损坏3个磁盘的概率。
那么1小时之内3个盘同时损坏的概率是多少呢？

磁盘故障/损坏的概率一般是按“泊松分布（Poisson Distribution）”来计算。“泊松分布”是指单位时间内独立事件发生次数的概率分布。下面就是泊松分布的公式：等号的左边，P表示概率，N表示某种函数关系，t表示时间，n表示数量；等号的右边，λ表示事件的频率。

泊松分布的详细介绍可以参考：https://zh.wikipedia.org/wiki/泊松分佈和https://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html。本文只给出计算结果。

对 zStorage 的3副本存储来说，1小时内发生3次“不同的”磁盘损坏事件的概率就表示为 P(N(1) = 3)。假设SSD磁盘的年化故障率为1.5%。

参考backblaze的2023年年中磁盘统计报告，我们选择了磁盘数使用时间较长的统计https://www.backblaze.com/blog/ssd-edition-2023-mid-year-drive-stats-review/

下面我们用一套典型的 zStorage 分布式存储集群配置来计算在1小时之内3块磁盘的损坏概率：

  • 存储节点数：3个

  • 每个存储节点16块磁盘，共48块磁盘

  • 磁盘大小3.84TB

  • 副本数：3

  • AFR即年化磁盘故障率：1.5%
用如下的 python 代码来计算：
#!/usr/bin/python
# -*- coding: utf-8 -*-
import decimal    
import math    
import time    


def  KdiskFailRate(N, T, ARF, K):
    # λ：每小时的坏盘数量
    lambda1 = decimal.Decimal(str(N*AFR/24/365))        
    return poisson(lambda1, T, K)   


#级数
def factorial(n):
  S = decimal.Decimal("1")      
  for i in range(1, n+1):
    N = decimal.Decimal(str(i))
    S = S*N      
  return S    


#泊松分布
def poisson(lam, t, R):
    e=decimal.Decimal(str(math.e))        
    return ((lam * t) ** R) * (e**(-lam*t))  factorial(R)    




N = 48
RepNum = 3
T = 1
AFR = 0.015


failRate=KdiskFailRate(N,T,AFR,RepNum)
print "KdiskFailRate: " ,failRate
代码输出的结果是：
KdiskFailRate: 9.253333714840863022098285545e-14
即这套 zStorage 分布式存储集群配置下，1小时内坏3个盘的概率是9.25e-14。
那么，是否可以得出结论，认为这套分布式存储系统在1小时内数据丢失的概率为9.25e-14？
答案是不能，因为3个磁盘在1小时内损坏并不一定会导致数据丢失。比如说坏的3个盘中，有2个盘是在同1个存储节点（数据分布不会把数据的相同副本放在同1个存储节点上），因此还有如下结论：
结论二：数据丢失的概率还要计算某个时间内磁盘“同时”损坏时命中数据的所有副本的概率。
我们来看如下一个示意图，假设3个存储节点，每个节点4个磁盘：
在上图中，我们假设磁盘是用1对1镜像的方式，而不是分片的方式进行冗余。即3个节点的Disk1在3个存储节点上是3个副本的1对1镜像，Disk2是3个副本的1对1镜像等等（图中我们用同一种颜色表示磁盘处于同一个镜像中）。这不就是类似RAID1的磁盘镜像吗？确实就是这个冗余的方式。
所以如果是节点1的Disk1先损坏，接下来只有当节点2和节点3的Disk1都相继坏了，才会产生数据丢失。
但假设磁盘损坏的顺序是节点1的Disk1、节点2的Disk1、节点3的Disk2，则不会产生数据丢失。因为在节点3上还有Disk1的副本，节点1和2上还有Disk2的副本。
所以在上面的示意图中，只有4种组合，会导致数据丢失和损坏。那么这种情况下，“同时”损坏3块盘的所有组合有多少呢？答案是一共220种。这是一个组合数学，即12个磁盘中选择3个盘的组合数，公式为：

其中：
  • n是磁盘总数（这里是12个磁盘）
  • k是选择的数量（这里是3个磁盘）
  • ! 表示阶乘
用 python 代码写出来就是：
def C(n, m):
  return factorial(n)  (factorial(m)*factorial(n-m))  


def factorial(n):
  S = decimal.Decimal("1")      
  for i in range(1, n+1):
    N = decimal.Decimal(str(i))
    S = S*N      
  return S    
所以上述220种组合中只有4种组合的情况下才会导致数据丢失。
如果对磁盘进行分片再做副本镜像，又是怎样的情况呢？示意图如下：
在上图中，我们将每个磁盘分成了4片，每片是一个“数据副本”，每个分片的副本分布在3个节点“随机”的磁盘上。以上图为例，节点1的Disk1的第1个分片“A”，对应的数据副本在节点2的Disk2和节点3的Disk4上。
所以数据分片副本随机地放在磁盘上，但即使是随机分布，由于分片数量有限，也并不是“同时损坏”3个磁盘一定会导致数据丢失。在上图中，节点1的Disk1、节点2的Disk2和节点3的Disk4“同时损坏”，会导致“A”分片的所有副本丢失，进而导致数据丢失。但是如果是节点1的Disk1、节点2的Disk2和节点3的Disk3“同时损坏”，并不会导致数据丢失，此时损坏磁盘的数据还有副本在其他磁盘上。
那这种情况下，3个磁盘“同时”损坏导致数据丢失的组合应该是多少呢？要计算这个组合数，我们不妨换一个逻辑来计算：

  • 当某个数据分片的3个副本全部丢失会导致数据丢失。

  • 而有多少个数据分片就意味着有多少个组合。
计算一下：
  • 共3个存储节点，每个存储节点4个盘，每个盘有4个数据分片的副本，所以副本总数为3存储节点*4个盘*4个数据分片副本=48个数据分片副本。
  • 48个数据分片副本/3副本数=16个数据分片。
也就是说，在上面的示意图中，有16种组合，会导致数据丢失和损坏。
如之前计算，3个存储节点、每个节点4个盘，即12个磁盘坏3个盘的组合数为220种。220种组合中只有16种组合的情况下有3个磁盘损坏才会导致数据丢失。
回到典型的分布式存储配置中，如果有3个存储节点，每个存储节点16个盘，共48个盘。整个存储池有512个数据分片，每个数据分片3个副本。我们来计算有多少种组合的3个磁盘“同时损坏”会导致数据丢失：
  • 如之前计算，512个数据分片意味着有512种组合，会导致数据丢失和损坏。
  • 48个磁盘中“同时”损坏3个磁盘的组合数是17296。
  • 也就是说，3个磁盘即使“同时”损坏，也只有512/17296= 0.029602220166512的概率会丢失数据。
  • 所以最终结论是：数据丢失的概率应该为 9.25e-14*0.0296=2.738e-15
注意，这是1小时之内“同时”有3个磁盘损坏导致数据丢失的概率。如果是计算1年的数据丢失概率呢，用如下的代码：
def LoseRate(LossDataRateInT):
    return 1 - (1 - LossDataRateInT)**(365*24/T)

得到的结果是：2.431e-11

说明：网上有别的文章在计算时，会考虑“同时”坏4个盘、5个盘等情况的概率，然后进行累加。不过这个概率更小，最终结果的差别可以忽略，所以为了简单起见，忽略这些情况。

本文一直说的是数据可靠性，实际上用“1-数据丢失的概率”就是数据可靠性概率：1-(2.431e-11)=0.99999999997569。按百分比表示就是99. 999999997569%，实际上已经达到了10个9，超过了文章开头所提到的9个9的可靠性。
我们再计算一下其他配置下的数据丢失概率：
配置1
5个存储节点，每个存储节点24个盘，3副本，磁盘年化损坏率为1.5%，存储池分为512个分片，单个磁盘损坏重构时间为1小时。
计算过程：

  • 磁盘总数为5*24=120个

  • 1小时内坏3个磁盘的概率：1.445655e-12

  • 3个磁盘“同时”损坏导致数据丢失的组合有512个

  • 120个磁盘损坏3个磁盘的组合数有280840

  • 因此3个磁盘在1小时内损坏导致数据丢失的概率为(1.445655e-12)*512/280840=2.635577e-15

  • 年度内损坏3个磁盘导致数据丢失的概率为：2.33413e-11

  • 即年度内数据可靠性为：99.99999999766587%
    结论仍然是10个9的可靠性！
配置2
3个存储节点，每个存储节点16个盘，3副本，磁盘年化损坏率为1.5%，存储池分为16个分片，单个磁盘损坏重构时间为1小时。
这个配置即本文第1个示意图，使用磁盘镜像的方式。我们来看一下计算过程：

  • 磁盘总数为3*16=48个

  • 1小时内坏3个磁盘的概率：9.253333715e-14

  • 3个磁盘“同时”损坏导致数据丢失的组合有16个

  • 48个磁盘损坏3个磁盘的组合数有17296

  • 因此3个磁盘在1小时内损坏导致数据丢失的概率为(9.253333715e-14)*16/17296=8.5599757e-17

  • 年度内损坏3个磁盘导致数据丢失的概率为：9.725554e-13

  • 即年度内数据可靠性为：99.99999999990274%
    结论是高达12个9的可靠性！
我们通过计算过程，可以得到结论三。
结论三：数据分片数量越少，即每个数据分片包含的数据量越大，数据丢失的概率越小。
数据分片数量越少，磁盘损坏时命中3个副本同时坏的组合数就越少，也就是数据丢失的概率越小。
除了数据分片数，还有影响数据丢失概率的其他变量，其中一个是磁盘重构时间。如果由于磁盘很大，或者重构速率低，导致重构时间变长，比如变为8小时，我们来看看数据丢失的概率：
配置3
5个存储节点，每个存储节点24个盘，3副本，磁盘年化损坏率为1.5%，存储池分为512个分片，单个磁盘损坏重构时间为8小时。
本配置跟“配置1”的变化是磁盘重构时间从1小时变为了8小时，计算过程如下：

  • 磁盘总数为5*24=120个

  • 8小时内坏3个磁盘的概率：7.39111566452e-10

  • 3个磁盘“同时”损坏导致数据丢失的组合有512个

  • 120个磁盘损坏3个磁盘的组合数有280840

  • 因此3个磁盘在8小时内损坏导致数据丢失的概率为(7.39111566452e-10)*512/280840=1.3474758653447657e-12

  • 年度内损坏3个磁盘导致数据丢失的概率为：1.47548806506137e-9

  • 即年度内数据可靠性为：99.99999985245119%
    结论是8个9的可靠性，比“配置1”的可靠性低了2个数量级。
其他条件不变，如果我们把单个磁盘重构时间延长为24小时，则年度的数据丢失概率为1.32357896e-8，即数据可靠性为99.9999986764%，7个9的可靠性。这相比1小时的重构时间，可靠性下降3个数量级。
因此我们又得到一个结论：
结论四：磁盘故障重构时间变长，数据可靠性下降，重构时间从1小时到24小时，可靠性下降3个数量级，即下降1000倍。
另一个影响变量是副本数，如果是从3副本变为2副本，这个影响比较巨大。
配置4
5个存储节点，每个存储节点24个盘，2副本，磁盘年化损坏率为1.5%，存储池分为512个分片，单个磁盘损坏重构时间为1小时。
计算过程：

  • 磁盘总数为5*24=120个

  • 1小时内坏2个磁盘的概率：3.37496933e-7

  • 2个磁盘“同时”损坏导致数据丢失的组合有512个

  • 120个磁盘损坏2个磁盘的组合数有7140

  • 因此2个磁盘在1小时内损坏导致数据丢失的概率为(3.37496933e-7)*512/7140=2.420146e-8

  • 年度内损坏2个磁盘导致数据丢失的概率为：0.00021198232027497266

  • 即年度内数据可靠性为：99.9788%
    结论是接近于5个9的可靠性，这是网上提到2副本5个9可靠性的由来。
所以2副本与3副本相比，可靠性有4个数量级的下降，但实际上还是相当可靠。我转换一下说法，年度数据丢失概率是0.00021198232027497266，实际上是指100年的时间内数据丢失概率为2%，10000年的时间内数据丢失概率为88%。
如果其他条件不变，但是磁盘重构时间变为24小时，年度的数据丢失概率就为0.000316653，概率提升了1.5倍，没有像3副本那样的数量级差异。
所以可以得出下个结论：
结论五：2副本相比3副本，数据可靠性降级4个数量级，即1万倍的差距。
关于这个结论的运用，可以考虑到副本数动态变化的情况：
  1. 对于上述讨论的“配置1”，如果1个存储节点故障，存储池退化为2副本，zStorage 设计为默认情况下如果7天内存储节点还没有修复，则开始启动重构。7天内数据可靠性为2.55e-7，可靠性仍然很高。
  2. 对于上述讨论的“配置4”，如果1个存储节点故障，存储池退化为1副本，zStorage 设计为默认情况下如果24小时内存储节点还没有修复，则开始启动重构。1天内数据丢失的概率为0.003945，即30天内数据丢失的概率是11.2%，90天内数据丢失的概率是29.9%，还是存在较高的风险。也就是说，如果2副本存储池在一个节点故障的情况下，3个月还没有修复，则有29.9%的概率会出现再坏一个盘而导致数据丢失。所以要尽可能快速修复节点，或者是有更多的存储节点，保证有足够的剩余空间进行一个节点数据的重构。这样的情况下，即使节点故障长时间没有修复，安全性还是很高。
那么有人可能会说，2副本风险较高，是不是不安全？安全是相对的，我们可以计算下RAID 10模式，即同样是2副本的数据可靠性。有如下的配置：
  • 8个盘为一组做了一个RAID 10，每个盘大小为4TB，一共15组，共120个盘。
  • 有1个热备盘，故障后能够自动进行重构
  • 磁盘的故障率AFR仍然为1.5%
  • 磁盘的重构速率为200M/s
所以磁盘的重构时间为5.7小时，按6小时算，按同样的计算过程：
  • 磁盘总数为121个
  • 6小时内坏2个磁盘的概率：7.717518123e-7
  • 2个磁盘“同时”损坏导致数据丢失的组合有60个
  • 121个磁盘损坏2个磁盘的组合数有7260
  • 因此2个磁盘在6小时内损坏导致数据丢失的概率为(7.717518123e-7)*60/7260 = 6.3781142e-9
  • 年度内损坏2个磁盘导致数据丢失的概率为：9.312e-6

  • 即年度内数据可靠性为：99.999%

    结论是5个9的可靠性，比2副本可靠性略高，但几乎处于同一水平。

如果把RAID 10变为RAID 5，因为RAID 5的重构速率更低，假设为100M/s，则重构时间为12小时。计算如下：
  • 磁盘总数为121个
  • 12小时内坏2个磁盘的概率：0.00000308
  • 2个磁盘“同时”损坏导致数据丢失的组合有420个
  • 121个磁盘损坏2个磁盘的组合数有7260
  • 因此2个磁盘在12小时内损坏导致数据丢失的概率为(0.00000308)*420/7260=1.78182e-07
  • 年度内损坏2个磁盘导致数据丢失的概率为：0.00013
  • 即年度内数据可靠性为：99.987%
    这几乎与2副本的分布式存储相同。
分布式存储和RAID盘的对比，其结论是：RAID 10的可靠性略好于2副本的分布式存储，而RAID 5的可靠性与2副本的分布式几乎相同。
不过这都是理论上的计算，在实际情况下，RAID是要依赖于热备盘或者及时更换磁盘才能进行重构，而分布式存储不需要热备盘则可进行重构。假设RAID 10没有热备盘，需要在磁盘故障时进行磁盘替换，替换时间+重构时间=24小时，则年度数据丢失概率变成3.71129e-5，比9.312e-6低了不少。
综合上述所有讨论，最终结论是：
  1. 分布式存储的数据可靠性跟磁盘故障率、磁盘损坏后的重构时间、副本数、分片数、磁盘数都有直接的关系。
  2. 总数量为N个磁盘的分布式存储在磁盘重构时间T内，R（R为副本数）个磁盘同时损失导致的数据丢失概率的主要公式为“R个磁盘在T时间内同时损坏的概率”*“R个磁盘同时故障命中同1个数据分片的所有副本的概率”。公式的前一部分根据泊松算法和磁盘年度故障率来计算，后一部分用“分片数/N个磁盘内故障R个磁盘的组合数”来计算。
  3. 3副本的数据可靠性非常高，年度内9个9以上的可靠性，基本上来说不会有丢失数据的可能性。
  4. 2副本的数据可靠性相比3副本来说有4个数量级的差距，即5个9的可靠性，所以一定要保留足够的剩余空间能够让磁盘损坏时顺利进行重构，即2副本的存储池不能将空间用得太满。
  5. 如果是2副本存储池，假设一个存储节点故障，如果没有足够的空间来进行数据重构，此时只剩余1个副本，数据可靠性风险就相当高。所以一定要及时修复故障的存储节点，或者是有较多的剩余空间可以进行重构，这样就有比较高的安全性。

  6. 3副本存储池，如果出现存储节点故障，数据副本数退化为2副本，数据的可靠性仍然很高，即使没有剩余空间进行重构，也非常安全，有足够长的时间可以进行节点修复。

上一篇： 站在DeepSeek的肩膀上，我用zCloud看到企业级SQL性能优化的更多可能性
下一篇： 让数据库起飞的存储底座怎么选？你只需掌握这六点